Matrix exponentiation to solve linear recurrence

The last weekend i was trying to solve a problem called Circle Summation on interviewstreet.com, if you have account you can view it using this link. However the problem is that we have N children sitting along a circle, numbered 1,2,...,N clockwise. The i^th child has a piece of paper with number a_i written on it.  They play the following game:

In the first round, the child numbered x adds to his number the sum of the numbers of his neighbors. In the second round, the child next in clockwise order adds to his number the sum of the numbers of his neighbors, and so on. The game ends after M rounds have been played.

Given N, M, and X's, Formulate the following output:

Output N lines each having N integers. The j^th integer on the i^th line contains the number that the j^th child ends up with if the game starts with child i playing the first round. Output a blank line after each test case except the last one. Since the numbers can be really huge, output them modulo 1000000007.  

As you can see we can represent this problem as a linear recurrence where F(N) = F(N-1) + F(N) + F(N+1).

A linear recurrence is a sequence of numbers, in which we can compute the nth term from the existent of other terms (e.g., Fibonacci sequence).

For example in the fibonacci series we can represent the sequence using the following recurrence equation:

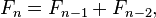Where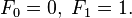 

Now by looking into the following recurrence we can represent it with this equation x_i+1 = Mx_i, for some constant matrix M.

| f(n+1) | = | 1 1 | x | f(n)   |
| f(n)   |   | 1 0 |   | f(n-1) |        => (1)

From (1) We can see that we can find F(N), by solving M^n. (Prove it, using math induction).

By analyzing the previous equation we can find that we will do O(M^3) operations for matrix multiplication where M is a very small number, and for the power function we can do it in O(Log(N)) operations, that will lead us to O(M^3 Log(N)) to solve fibonacci numbers.

Now, Can you solve the circle summation problem? :).. I solved it..